Heap Sort

algorithm, heap, sort

Complete Binary Tree

一株二元樹（Binary Tree）若依序由左而右、由上而下排列，且除了最後一層外其餘層數皆排滿，即為 Complete Binary Tree 。

若第一個節點編號為 1 ，則從 Complete Binary Tree 任取一節點編號 k ，該節點的父節點、左邊子節點、右邊子節點都可以用公式表示：

父節點： k / 2 後無條件捨去
左邊子節點： k * 2
右邊子節點： k * 2 + 1

如下圖：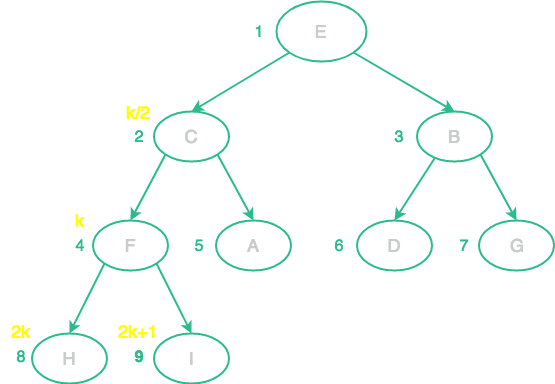

這個特性讓該資料結構可以被放在陣列之中運算。

Heap （堆積）

Heap 是一種以 Complete Binary Tree 做為骨架的資料結構，分為兩種：

Max Heap

每個父節點的值永遠大於子節點。
公式： Value[k / 2] > Value[k]

Min Heap

每個子節點的值永遠大於父節點。
公式： Value[k / 2] < Value[k]

使用 Heap 的好處是，位於節點編號 1 的值永遠都是最小值或最大值，因此對於 Heap 來說，要得到資料的極值是很方便的事。

Heapify

在進入 Heap Sort 之前必須先知道如何將陣列資料轉為 Heap。假設一組由兩個子節點加上一個父節點所組成的小型二元樹。

Heapify 的過程是將父節點與左子節點和右子節點比較，以 Max Heap 舉例，若最大值出現在某個子節點，則把該子節點的值與父節點的值互換。

由於被更換後的子節點也可能是別人的父節點，因此必須找到該子節點為父節點的小型二元樹，重複最大值的檢查與交換，以此向下層類推，這就是 Heapify 的過程。

如下圖：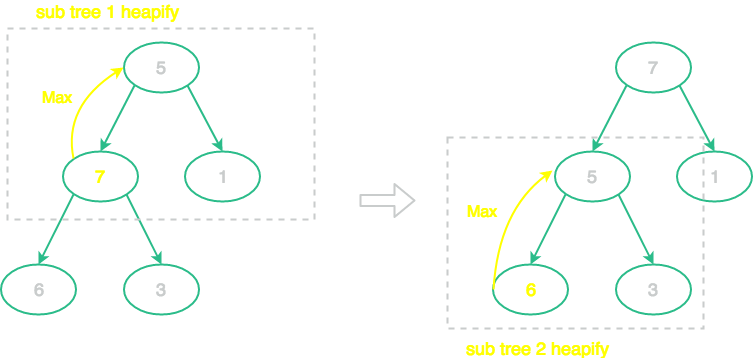

Build a Heap

要將一段長度為 N 隨機數組轉換成 Heap ，只要從 2/N （若為奇數則無條件捨去）處開始 Heapify 到第一筆資料就好。

為何是 2/N ？ 上面有提到 Complete Binary Tree 的任一節點 X 的父節點位置為 2/X ，反過來說，也只有 2/N 以下的數字才會有子節點，有子節點才有做 Heap 的意義。

Heap Sort （堆積排序）

概念

Heap Sort 就是利用 Heap 資料結構的特性來對一串數列進行排序的演算法。舉例來說，若有一串數列是以 Min Heap 的方式排列，其編號為 1 的節點的值永遠是最小值。

因此只要把編號為 1 的節點的值取走，然後將剩下的數列重新排為 Heap ，編號為 1 的節點又會再次出現剩餘資料的的最小值，重複「取走、重排」動作至最後一筆資料，就可以完成排序。

整個程式分三部分：

  • Build Heap：將陣列資料轉換成 Max Heap 資料結構
  • Swap：把在節點 1 產生的最大值換到底部，將其視作已排序的值，不再動它
  • Heapify：把剩下的數字重新轉換成 Max Heap，使新的最大值產生

流程圖

程式碼

在 heapSort 前段，我們刻意在隨機數組前插入一個任意欄位。這是因為 Heap 只有在節點編號從 1 開始算起時，父節點與子節點間才會有上述公式的關聯性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 隨機陣列
let randomData = [5, 8, 3, 4, 7, 1];
let size = randomData.length;

// 定義 heapify
function heapify(Arr, index, size) {
  // 利用節點關聯性的公式來鎖定左右子節點的位置
	let left = index * 2;
  let right = index * 2 + 1;
  let max = index;
  if(left <= size && Arr[index] < Arr[left]) {
  	max = left;
  }
  
  if(right <= size && Arr[max] < Arr[right]) {
  	max = right;
  }
  
  if(max !== index) {
  	let temp = Arr[index];    
    Arr[index] = Arr[max];
    Arr[max] = temp;
    heapify(Arr, max, size);
  }
}

// 定義 build heap
function buildHeap(array, size) {
	for(let i = Math.floor(size / 2); i > 0; i--) {
  	heapify(array, i, size);
  }
  return array;
}

function heapSort(array) {

  // 為了讓數組從 1 開始算，而插入欄位
	let result = array.slice();
  result.unshift(0);
  
  result = buildHeap(result, size);
  for(let i = size; i > 0; i--) {
  	let temp = result[i];
    result[i] = result[1];
    result[1] = temp;
		heapify(result, 1, i-1);
  }
  console.log(result)
}

heapSort(randomData)

Reference

  1. GeeksForGeeks Heap Sort Video
  2. ChiuCC’s blog article